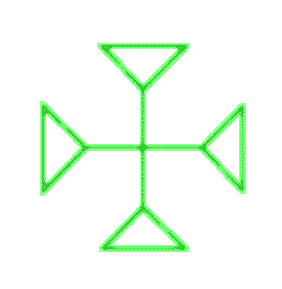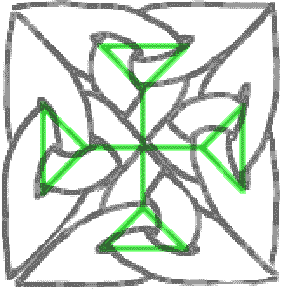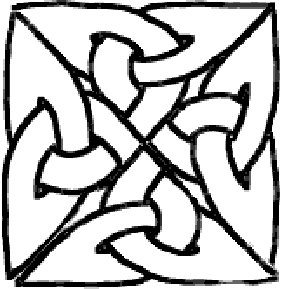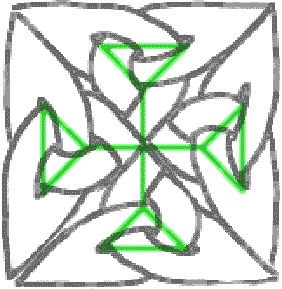
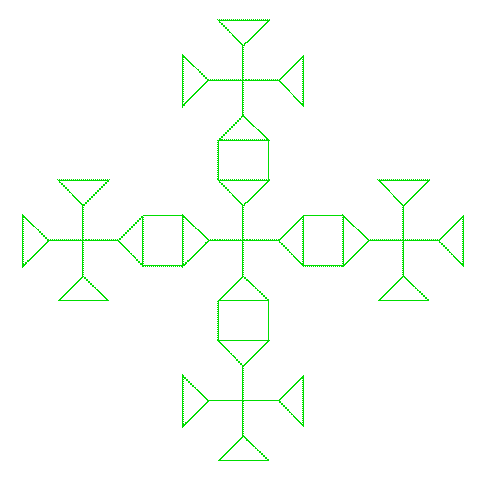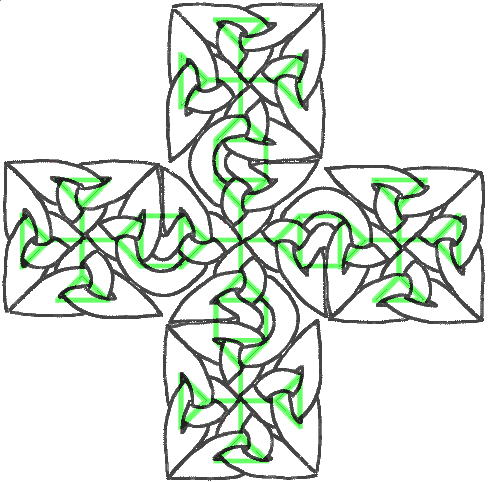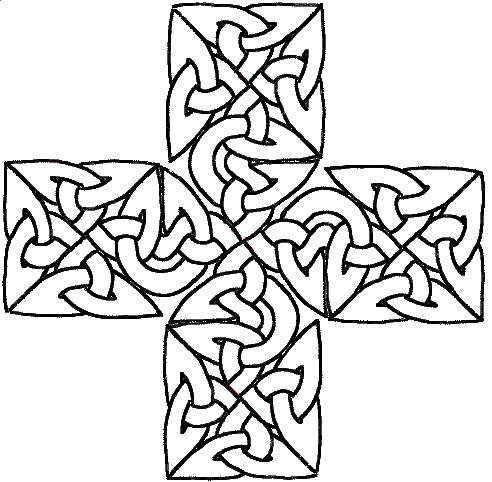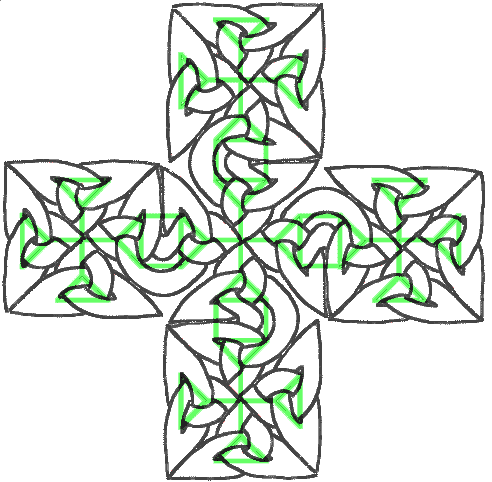
Vous allez apprendre comment mettre en boîte un motif, ce que j’appelle "l’encapsuler", de manière à pouvoir l’utiliser dans une création plus grande. Nous commençons d’abord par découvrir qu’il y a un besoin sur un exemple. Disons que vous aimez le nœud de trèfle (c’est mon cas) et que vous voulez en faire quelque chose. Par exemple une croix. Le trèfle étant codé par un triangle, vous pouvez essayer de mettre quatre triangles côtes à côtes et après beaucoup de peine et de sueur, vous pouvez obtenir quelquechose comme ça :
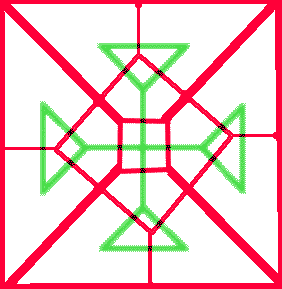
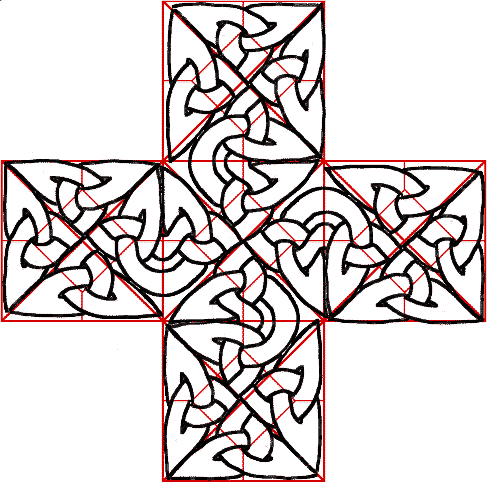
C’est très joli mais nécessite beaucoup de coup de main. Vous pouvez essayer d’aller plus loin et en faire le motif d’une plus grande croix. Après beaucoup de gros mots et de ratures, vous obtiendrez par exemple :
Très joli, mais vraiment dur à ajuster. Si vous essayez, vous verrez qu’on ne peut pas faire de grandes figures précises de cette façon. Heureusement, il y a une méthode pour ne pas tatonner, celà s’appelle l’encapsulation. Mais tout d’abord il faut que vous compreniez une notion mathématique assez simple mais vraiment riche :
La dualité
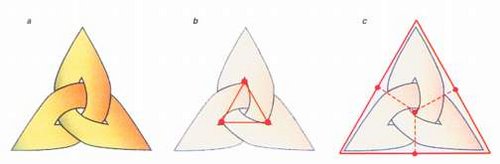
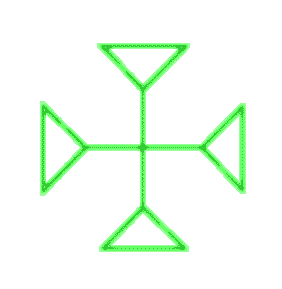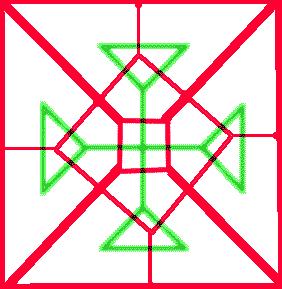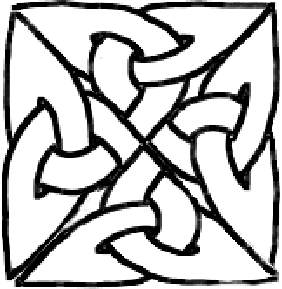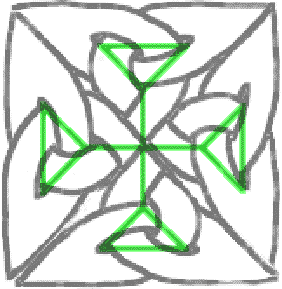
En reprenant le nœud de trèfle, quand vous en extrayez le graphe, vous auriez pû mettre les sommets non pas dans les zones blanches mais dans les zones noires. La zone externe est un peu spéciale, il faut fusionner tous les sommets qu’on place naturellement à l’extérieur près de chaque croisement, en un seul en les connectant par un grand mur qui fait tout le tour du motif. Sur la sphère, nous n’aurions pas ce problèmes. Une image valant mieux que de longs discours, on obtient la figure c., au lieu de la figure originale b. :
Vous venez d’assister à la construction du dual du triangle. En fait, une fois que vous avez le graphe, vous n’avez plus besoin du nœud, vous pouvez construire son dual directement : Ses sommets sont au centre des faces du graphe de départ et ses arêtes sont transverses :
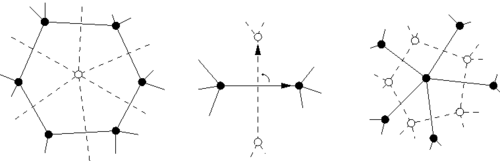
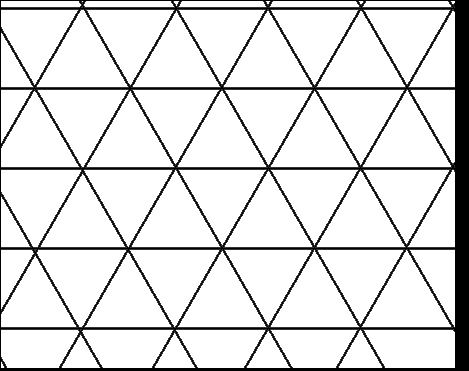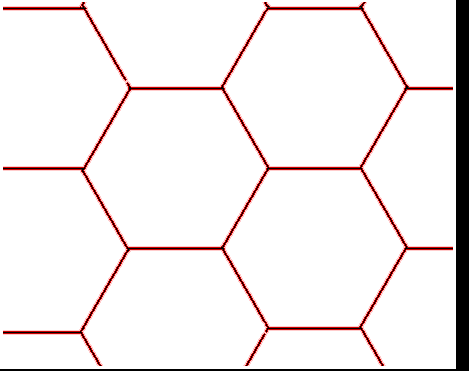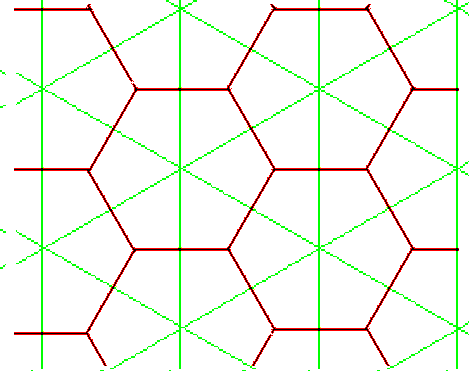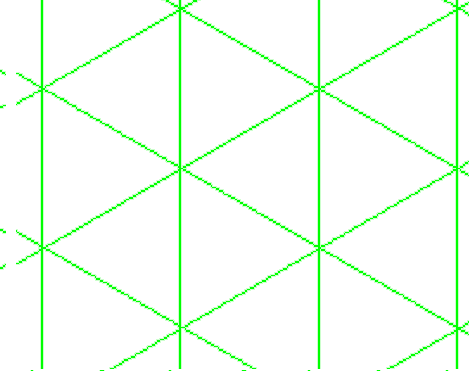
Par exemple, le réseau triangulaire est dual du réseau hexagonal (cliquez dessus).
Maintenant vous voyez que notre nœud de trèfle étant complètement enfermé dans une boîte, c’est très simple de l’utiliser pour faire une croix. Il suffit de dessiner un carré, ses diagonales, ce qui fait quatre capsules triangulaires, de recopier à l’intérieur le graphe du nœud de trèfle, d’ouvrir quelques murs pour que les nœuds se fondent en un seul et voila !
Quant à la grande croix c’est encore plus facile, empilez cinq de ces carrés et ouvrez quelques murs pour que les petites croix se mélangent :
L’idée derrière la construction d’un grand motif est de commencer par trouver des petits nœuds que vous aimez, de les mettre en boîte en construisant leur graphe dual et de paver votre espace de travail avec ces boîtes.
Voyons un autre exemple. En jouant avec le réseau triangulaire, vous trouvez ce joli motif :
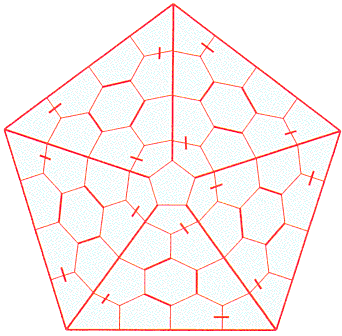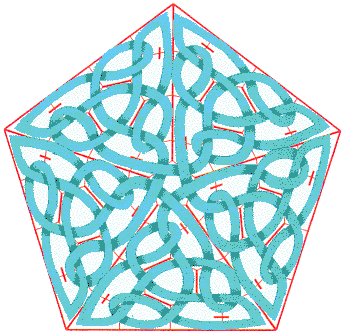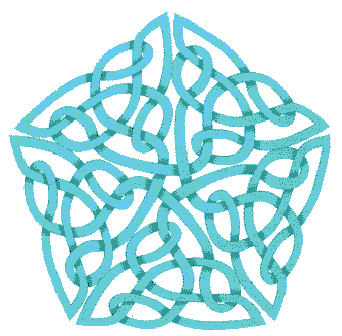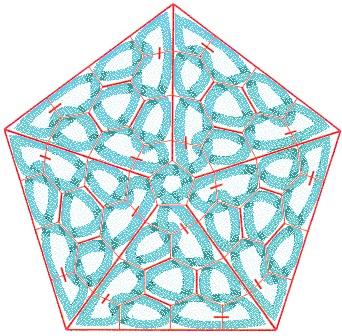
Pour en faire quelque chose, il faut d’abord construire son graphe dual (cliquez dessus) :
Ensuite vous pouvez en faire une croix à cinq branches en claquant des doigts :
La seule difficulté réside dans le choix des portes à ouvrir dans les murs d’enceinte entourant vos capsules. Il en faut suffisament pour que vos noeuds se mélangent mais néanmoins judicieusement placées pour que chaque motif soit reconnaissable. C’est comme un mariage réussi, il faut qu’ils ne forment qu’un tout en gardant leur individualité.
Maintenant, si vous voulez des entrelacs qui ont un début et une fin, il vous faut des enchevêtrements.